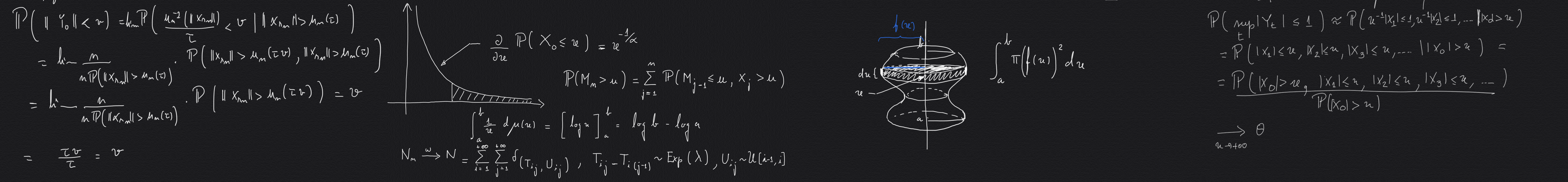
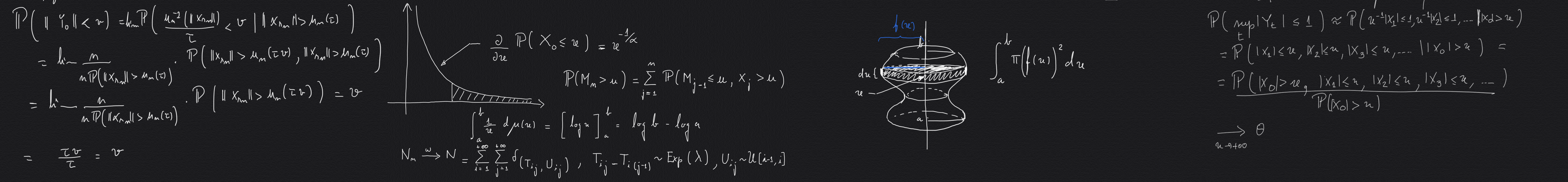
Project funded by FCT (Portugal). Information on the FCT website can be found here.
In general terms the goal of this project is to study statistical properties of Dynamical Systems (DS), both deterministic and stochastic, with special emphasis on laws of rare events.
The emergence of chaos and its associated unpredictability brought light to Probability and Ergodic Theory as tools to analyse the behaviour of chaotic systems. This means that statistical properties of chaotic systems have become a master key for the understanding of the long term evolution of such systems. The existence of invariant measures with physical relevance, ergodicity, mixing, large deviations, laws of large numbers, limit theorems, have been exhaustively studied during the last decades.
Among such limit laws, which include Central Limit Theorems, we are particularly interested in limit laws for exceptional events. The recurrence effect introduced by Poincaré, which is present in chaotic systems, is the starting point for a deeper analysis of the limit distribution of the elapsed time until the occurrence of a rare event, which is usually referred to as Hitting Time Statistics (HTS) and Return Time Statistics (RTS). This is a recent topic started in the nineties of the last century and our team includes two world’s recognized specialists in the subject.
The study of extreme or rare events is of great importance in a wide variety of fields and is often tied in with risk assessment. This explains why Extreme Value Laws (EVL) and the estimation of the tail limit distribution of the maximum of an arbitrarily large number of observations has drawn much attention and become a highly developed subject. In many practical situations, such as in the analysis of financial markets or climate phenomena, time series can be modelled by a dynamical system, which describes its time evolution. Surprisingly, EVLs for dynamical systems is an even a more recent topic dating back to the pioneer paper of Collet in 2001. Since then, the members of the team have played a crucial role in the development of the theory of EVLs for stochastic processes arising from chaotic deterministic dynamics.
In our opinion, a major breakthrough was achieved by establishing a connection between HTS/RTS and EVLs for dynamical systems. In [FFT10], the authors show that existence of HTS/RTS implies the existence of an EVL and vice-versa. This means that results of EVLs can be proved using tools from HTS/RTS and the other way around.
A major goal of the project is then to carry the theory further. Namely, to apply it to different types of dynamical settings, to exploit the connection mentioned above and elaborate on this possibility of knowledge interchange.
In order to prove such type of results, one has to study the dependence structure of the stochastic processes obtained from the dynamical systems. In particular, the dependence of the random variables should fade away as they become further and further apart. This phenomenon is linked to the rates of mixing or decay of correlations of the system. Hence, understanding these properties of the systems and their relation with other statistical quantities such as large deviations and the mechanisms that generate them is also a goal of the project.
Another major issue has to do with the stability of the systems when random noise is introduced. These stochastic dynamical systems resulting from perturbing a deterministic one provide in many situations a better application to real life phenomena. Understanding if these statistical properties prevail under random perturbation and developing a theory of rare events for such stochastic systems is one of the main objectives.
Finally, estimation of tail indices and applications of the theory to risk models is another goal of the program.
