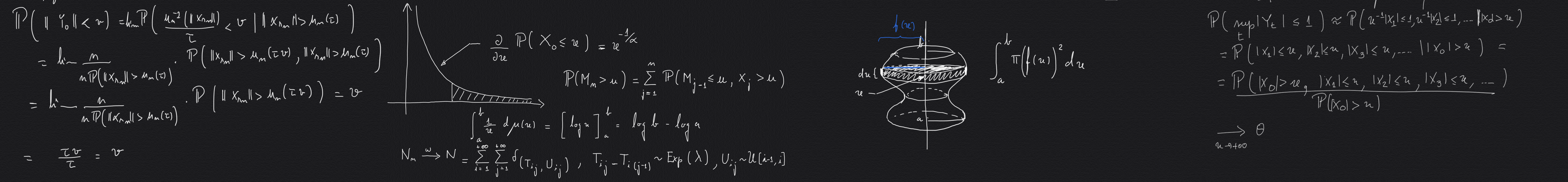Limiting laws ruling dynamical systems
Reference: PTDC/MAT-PUR/28177/2017
Budget: 213.783,22 Euro
Starting date: 2018-10-04 End date: 2022-10-03
Project funded by FCT (Portugal).
Principal Investigator
Co-Principal Investigator
Team Members
Summary
In general terms, the main goal of this project is to study statistical properties of dynamical systems, which are particularly
captured by the description provided by limiting laws.
The complexity of the orbital structure of chaotic systems brought special attention to the existence of such limiting laws,
since they borrow at least some probabilistic predictability to the erratic behaviour of such systems.
The first step in this direction is the construction of invariant physical measures, which provide an asymptotic spatial
distribution of the orbits in the phase space. Ergodicity then gives strong laws of large numbers.
The mixing properties of the system restore asymptotic independence and, in this way, allow to mimic iid processes and prove
limiting laws for the mean, such as: central limit theorems, large deviation principles, invariance principles, etc.
While the limiting laws mentioned so far pertain to the mean or average behaviour of the system, in the recent years, the study
of the extremal behaviour, ie, the laws that rule the appearance of abnormal observations along the orbits of the system has suffered
an unprecedented development, in which the team members took a prominent role. In this field of Extreme Value Theory applied to
dynamical systems, one is interested in the limiting law for the partial maxima of stochastic processes arising from the system.
It turns out that this study is deeply connected with the recurrence properties to certain regions of the phase space, which is
one of the most emblematic achievements of the team.
Part of the reason for the development of this field stems from the interest that Physicists working with meteorological data
saw in this area. One of the great advantages of understanding the extremal behaviour of dynamical systems is that the latter often
provide toy models for very complex physical phenomena. This is the case of the Lorenz equations, which show how a very simplified
model for the atmospheric convection can yet capture so accurately the complex and chaotic character of weather. Hence, the study of
this subject has direct applications to risk assessment associated with occurrence of meteorological abnormal phenomena.
The main purpose of this project is to carry further the study of the limiting laws for the average behaviour and the extremal
behaviour of the systems, as well as to understand the connection between both.
In particular, in the extremal case, we intend to provide more information about the impact of the occurrence of extreme events
and the structure of record observations, for which we plan to perform a more sophisticated analysis using tools such as the theory
of point processes. Moreover, in the case of heavy tailed distributions, which in this context are associated to observables with
polynomial type of singularities, the average is tied to the extremal behaviour. We intend to exploit this link and understand its
consequence in the dynamical setting.
Achievements
The main purpose of this project was the study of limiting laws describing the average and the extremal behaviour of chaotic system,
for which several particular goals and respective research plans were established.
During the project we managed to fully accomplish the proposed objectives and, in some topics, went far beyond them.
These achievements appeared published in several top journals of the field, such as Advances in Mathematics, Annals of Probability, Bernoulli, Communications in Mathematical Physics, Journal of the London Mathematical Society, Transactions of the American Mathematical Society, among others. Moreover, these findings were presented in international meetings and seminars at prestigious institutions in: France (CIRM, Institut de Mathématiques de Marseille, Université de Bretagne Occidentale, Université de Picardie Jules Verne, Université de Rennes 1), UK (ICMS - Edinburgh, University of Loughborough, University of St. Andrews, University of Warwick), Italy (Centro di Ricerca Matematica Ennio De Giorgi at Scuola Normale Superiore di Pisa), Austria (University of Wien), Sweden (Lund University), among others.
During the project 3 PhD students of the team defended their thesis. Moreover, the PI and co-PI are currently supervising 4 PhD students, who are pursuing research strands motivated by the work carried within the project. 2 of these 4 PhD students are previewed to defend their thesis during 2023.
Since the list of accomplishments is quite extensive, we make a brief review of the most relevant results and make a short description of the main achievements of the project. We use as a citation key the initials of the authors concatenated with the last two digits of the year of the publication. The details of each reference can be found below in the publications’ list.
- One of the first goals of the project pertained to the weak convergence of dynamically generated higher dimensional empirical Rare Events Point Processes (REPP), studied in [FFM20], where we considered empirical multi-dimensional rare events point processes that keep track both of the time occurrence of extremal observations and of their severity, for stochastic processes arising from a dynamical system, by evaluating a given potential along its orbits. This is done both in the absence and presence of clustering. A new formula for the piling of points on the vertical direction of bi-dimensional limiting point processes, in the presence of clustering, is given, which is then generalised for higher dimensions. The limiting multi-dimensional processes are computed for systems with sufficiently fast decay of correlations. The complete convergence results are used to study the effect of clustering on the convergence of extremal processes, record time, and record values point processes.
- We also highlight the limit theorems obtained for the two-dimensional random Lorentz gas, in [AL20], where we studied deterministic walks in random environment and showed that (in simple, yet relevant, cases) they can be reduced to a class of random walks in random environment where the jump probability depends (weakly) on the past. In addition, few basic results are proved (hopefully the germ of a general theory) for the latter purely probabilistic model.
- In [BLR19], we studied the behaviour of the shortest distance between orbits and showed that under some rapidly mixing conditions, the decay of the shortest distance depends on the correlation dimension. For irrational rotations, we proved a different behaviour depending on the irrational exponent of the angle of the rotation. For random processes, this problem corresponds to the longest common substring problem. The result of Arratia and Waterman on sequence matching to alpha-mixing processes with exponential decay was extended.
- This work was further deepened in [CLR20], where we investigated the length of the longest common substring for encoded sequences and its asymptotic behaviour. The main result is a strong law of large numbers for a re-scaled version of this quantity, which presents an explicit relation with the Rényi entropy of the source. This result is applied to the zero-inflated contamination model and the stochastic scrabble. In the case of dynamical systems, this problem is equivalent to the shortest distance between two observed orbits and its limiting relationship with the correlation dimension of the pushforward measure. An extension to the shortest distance between orbits for random dynamical systems was also provided.
- In [FFRS20], we studied the existence of limiting laws of rare events corresponding to the entrance of the orbits on certain target sets in the phase space. The limiting laws were obtained when the target sets shrink to a Cantor set of zero Lebesgue measure. We considered both the presence and absence of clustering, which is detected by the Extremal Index, which turns out to be very useful to identify the compatibility between the dynamics and the fractal structure of the limiting Cantor set. The computation of the Extremal Index is connected to the box dimension of the intersection between the Cantor set and its iterates.
- In [AFF20], we have shown how to build dynamically generated stochastic processes with an Extremal Index that does not coincide with the reciprocal of the mean of the limiting cluster size distribution. The mechanism used to build such examples is based on considering observable functions maximised at at least two points of the phase space, where one of them is an indifferent periodic point and another one is either a repelling periodic point or a nonperiodic point. This enables to mix the behaviour of an Extremal Index equal to 0 with that of an Extremal Index larger than 0. Using bi-dimensional point processes we explain how mass escapes in order to destroy the usual relation.
- In [AP21b], we considered some classes of piecewise expanding maps in finite dimensional spaces having invariant probability measures which are absolutely continuous with respect to Lebesgue measure. We derived an entropy formula for such measures and, using this entropy formula we presented sufficient conditions for the continuity of that entropy with respect to the parameter in some parametrized families of maps. We applied the results to a classical one-dimensional family of tent maps and a family of two-dimensional maps which arises as the limit of return maps when a homoclinic tangency is unfolded by a family of three dimensional diffeomorphisms.
- Finally, we mention the monograph [A21], which offers a coherent, self-contained account of the theory of Sinai–Ruelle–Bowen measures and decay of correlations for nonuniformly hyperbolic dynamical systems. A central topic in the statistical theory of dynamical systems, the book in particular provides a detailed exposition of the theory developed by L.-S. Young for systems admitting induced maps with certain analytic and geometric properties. Throughout the book, the theory is illustrated with applications. A clear and detailed account of topics of current research interest, this monograph will be of interest to researchers in dynamical systems and ergodic theory. In particular, beginning researchers and graduate students will appreciate the accessible, self-contained presentation.
Publications
- M. Abadi, A.C.M. Freitas, J.M. Freitas, Clustering indices and decay of correlations in non-Markovian models, Nonlinearity, 32, no. 12, 4853-4870, 2019.
- J. F. Alves, V. Ramos, J. Siqueira, Equilibrium stability for non-uniformly hyperbolic systems. Ergodic Theory Dynam. Systems, 39, no. 10, 2619-2642, 2019.
- J.F. Alves, M. A. Khan, Statistical instability for contracting Lorenz flows, Nonlinearity, 32, no. 11, 4413-4444, 2019
- V. Barros, L. Liao, J. Rousseau, On the shortest distance between orbits and the longest common substring problem, Advances in Mathematics, 344, 311-339, 2019.
- R. Aimino, J.M. Freitas, Large deviations for dynamical systems with stretched exponential decay of correlations, Portugaliae Mathematica, 76, no. 2, 143-152, 2019.
- V. Barros, R. Moura, G. Santos, Local well-posedness for the nonlocal derivative nonlinear Schrödinger equation in Besov spaces, Nonlinear Analysis, 187, 320338, 2019.
- A.C.M. Freitas, J.M. Freitas, and M. Magalhães. Complete convergence and records for dynamically generated stochastic processes, Trans. Amer. Math. Soc., 373,no. 1, 435–478, 2020.
- M. Abadi, A.C.M. Freitas, J.M. Freitas, Dynamical counterexamples regarding the extremal index and the mean of the limiting cluster size distribution, Journal of London Mathematical Society, 102, no. 2, 670-694, 2020.
- A.C.M. Freitas, J.M. Freitas, F.B. Rodrigues, J.V. Soares, Rare Events for Cantor Target Sets, Communications in Mathematical Physics, 378, 75-115, 2020.
- A.C.M. Freitas, J.M. Freitas, M. Magalhães, S. Vaienti, Point Processes of Nonstationary Sequences Generated by Sequential and Random Dynamical Systems, Journal of Statistical Physics, 181, no. 4, 1365-1409, 2020.
- R. Aimino, C. Liverani, Deterministic walks in random environment, Annals of Probability, 48, no. 5, 2212-2257, 2020.
- A. Coutinho, R. Lambert, J. Rousseau, Matching strings in encoded sequences, Bernoulli, 26, no. 3, 2021-2050, 2020.
- N. Haydn, J. Rousseau, F. Yang, Exponential Law for Random Maps on Compact Manifolds, Nonlinearity, 33, no. 12, 6760-6789, 2020.
- V. Barros, C. Nonato, C. Raposo, Global existence and energy decay of solutions for a wave equation with non-constant delay and nonlinear weights, Electronic Research Archive , 28, no. 1, 4205-220, 2020.
- A.C.M. Freitas, J.M. Freitas, J.V. Soares, Rare events for product fractal sets, J. Phys. A: Math. Theor., 54, no. 34, 245202, 2021.
- R. Aimino, M. Pollicott, Statistical Properties of the Rauzy-Veech-Zorich Map, in Thermodynamic Formalism, Lecture Notes in Mathematics, 2290, 317-349, Springer Cham. 2021.
- J.F. Alves, C.L. Dias, H. Vilarinho, On the liftability of expanding stationary measures, Stochastics and Dynamics, 21, no. 61, 2150039, 2021.
- J.F. Alves, A. Pumariño, Entropy formula and continuity of entropy for piecewise expanding maps, Annales de l´Institut Henri Poincaré (C) Analyse Non Linéaire, 38, no. 1, 91-108, 2021.
- J. F. Alves, Nonuniformly hyperbolic attractors. Geometric and probabilistic aspects, Springer Monographs in Mathematics, Springer,ISBN: 978-3-030-62814-7; 978-3-030-62813-0, 2020.
- J. Rousseau, Longest common substring for random subshifts of finite type, Ann. Inst. Henri Poincaré Probab. Stat., 57, no. 3, 1768-1785, 2021.
- J. Rousseau, Rényi entropy and pattern matching for run-length encoded sequences, ALEA, Lat. Am. J. Probab. Math. Stat. , 18, 887-905, 2021.
- V. Barros, J. Rousseau, Shortest distance between multiple orbits and generalized fractal dimensions, Ann. Henri Poincaré, 22, no. 6, 1853-1885, 2021.
- J. F. Alves; W. Bahsoun; M. Ruziboev, Almost sure rates of mixing for partially hyperbolic attractors, Journal of Differential Equations, 311, 98-157, 2022.
- J. F. Alves, D. Mesquita, Entropy formula for systems with inducing schemes, Transactions of the American Mathematical Society, https://www.ams.org/journals/tran/0000-000-00/S0002-9947-2022-08808-5/S0002-9947-2022-08808-5.pdf
Outreach in the radio
Leis de eventos raros em sistemas dinâmicos caóticos, 90 segundos de Ciência, Antena 1