Aula nº15

Cálculo simbólico (continuação)

Seguem-se as últimas instruções da aula anterior

> p:=x->1-x^2;

> a:=(k,n)->-1+2*k/n;

> sum((p(a(k,n))+p(a(k-1,n)))/n,k=1..n);

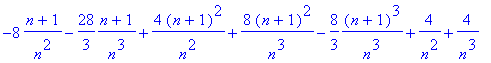
> simplify(%);

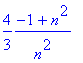
Qual é a área da região entre a parábola e o eixo dos xx? É dada por

> int(1-x^2,x = -1 .. 1);

É de esperar que este valor seja o limite da soma das áreas das figuras poligonais. De facto assim é, conforme se pode verificar fazendo

> limit(%%,n=infinity);

O Maple também pode ser empregue para calcular integrais impróprios:

> int(1/x^2,x=1..infinity);

bem como primitivas

> simplify(int(1/(cos(x)^2+4*sin(x)^2),x));

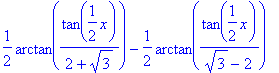
Para se definir esta primitiva como uma função, faz-se

> pr:=unapply(%,x);

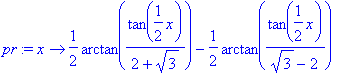
Isto permite «calcular» o valor do integral da função ao longo do intervalo. De facto, obtém-se um resultado incorrecto:

> pr(2*Pi)-pr(0);

Que isto não pode estar certo, resulta de a função só tomar valores positivos. Aliás, o seu gráfico pode ser visto fazendo

> plot(1/(cos(x)^2+4*sin(x)^2),x=0..2*Pi,view=[0..2*Pi,0..1]);

(a opção «view» é empregue para que os eixos se cruzem em (0,0)).

Repare-se que o Maple calcula correctamente o integral em questão.

> int(1/(cos(x)^2+4*sin(x)^2),x=0..2*Pi);

Isto pode ser calculado numericamente, bastando para tal fazer

> evalf(%);

ou, caso se queira ver o resultado com (por exemplo) 30 casas decimais

> evalf(%%,30);

Muitas vezes, é preciso restringir a um determinado conjunto os valores que uma variável pode tomar. Por exemplo, tem-se

> exp(ln(x));

mas

> ln(exp(x));

ou até

> simplify(ln(exp(x)));

Isto resulta da possibilidade de x não ser um número real. Se se quer impor que x seja real escreve-se

> assume(x,real);

Neste caso tem-se

> simplify(ln(exp(x)));

O ~ significa que se está a introduzir uma hipótese sobre x. Se se quer anular essa instrução, faz-se

> x:='x';

Resolução de equações

Considerem-se as seguintes definições:

> f:=x->x*sin(Pi*x);a:=1/2:b:=5/2:

Quer-se ilustrar o teorema de Lagrange; para tal, é preciso determinar o ponto do intervalo [a,b] tal que o declive da recta tangente ao gráfico de f nesse ponto seja igual ao declive do segmento que une (a,f(a)) a (b,f(b)).

> solve(D(f)(x)=(f(b)-f(a))/(b-a),x);

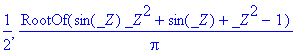
O método anterior não é o mais adequado; é preferível recorrer a métodos numéricos.

> so:=(f,a,b)->fsolve(D(f)(x)=(f(b)-f(a))/(b-a),x,a..b,maxsols=1);

A última opção garante que se obtém apenas uma solução.

> so(f,a,b);

> g:=x->f(so(f,a,b))+(x-so(f,a,b))*(f(b)-f(a))/(b-a);

> plot([f(x),g(x),[[a,f(a)],[b,f(b)]]],x=a-1..b+1,color=[red,green,blue],
view=[a-1..b+1,-3..3]);